The following are present in this first language:
- true and false.
- conditional expressions.
- The numeric constant 0.
- The arithmetic operators succ and prec.
- A testing operation iszero.
t = true
false
if t then t else t
0
succ t
prec t
iszero t
Programs
A program in the above language is a term built up from the forms given in the grammar.
if false then 0 else 1
1
1. Syntax
The grammar above is a way to specify the syntax of the language. One other way to do so is to specify it inductively using set theory.
Definition 1 Terms, Inductively: The set of terms is the smallest set
such that
- {true, false, 0}
.
- if
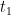
then succ(
), pred(
), iszero(
)
.
- if
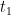
,
and
then if
then
else
.
Definition 2 Terms, By Inference Rules: The set of terms is defined by the following rules:
Rules set 1:
Rules set 2:
Rules set 3:
Each rule is read “If we have established the statements in the premise of the rules above, then the we may derive the conclusions in the lines below”. The rules with no premises are called axioms.
Definition 3 Terms, Concretely: The set of terms can also be given by constructing sets of successively bigger sizes.
For each natural number
we define a set
as follows:
Finally, let
Inference rules are just another way of writing the set theoretic definition.
Each inference rule may imply an infinite tree of terms.
Proposition 4
.
In definition on page we saw that a term can have one of three forms. This can be used in two ways:
- to give inductive definitions of functions over set of terms.
- in proving theorems about the properties of terms.
The consts, size and depth functions can be defined using inductive definition over the set of terms. Relations between sizes and depths, the cardinality of consts and size can be proven using the definition of the set of terms.
2. Semantic Styles
2.1. Operational Semantics
The behaviour of the program is described by specifying an abstract machine for it.
The machine is abstract in the sense that the terms of the program are what form the machine code, instead of some low level language.
The terms are represented by states of an abstract machine. The meaning of a program is represented by the output of the computation of the abstract machine whose starting state is the first term of the program, that is the value in the final state.
It is customary to give two or more different operational semantics for a single language. One closer to the language in question and the other closer to the machine language.
Proving that the above two operational semantics correspond in some suitable sense amounts to proving that the implementation is correct.
2.2. Denotational Semantics
It takes a more abstract view of meaning and instead of defining the meaning of terms in terms of a sequence of machine states, the meaning of term is defined to be some mathematical object – a function or a number.
3. Evaluation
Consider a language with grammar as below:
Syntax:
Values, a subset of terms, are the possible final outcomes of evaluation.
The evaluation relation is a binary relation on the set of terms.
Evaluation: t t‘
Definition 5 Evaluation Strategy: The interplay between the rules determines a particular order of evaluation.
Definition 6 Computation Rules:
Definition 7 Congruence Rules:
Definition 8 An instance of an inference rule is obtained by replacing the metavariables in the premises and conclusions of the rule.
Definition 9 A rule is satisfied by a relation if each instance of the rule the conclusion is in the rule or one of the premises is not.
Definition 10 A one-step evaluation relation
is the smallest binary relation on the set of terms which satisfies all the evaluation inference rules for the set of terms.
Definition 11 When a pair (t, t’) is in the one-step evaluation relation we say that the evaluation statement t
t’ is derivable .
Theorem 12 (Determinacy of One-Step Evaluation) If t
t’ and t
t”, then t’
t”.
Definition 13 A term t is in normal form if no evaluation rule applies to it, i.e.\, if there is no t’ such that t
t’.
Theorem 14 Every value is in normal form.
Theorem 15 If t is in normal form, then t is a value.
Definition 16 The multi-step evaluation relation
is the reflexive, transitive closure of the one-step evaluation relation. If t
t’ and t’
t”, then t
t”.
Consider a language with grammar as below:
Syntax:
Values, a subset of terms, are the possible final outcomes of evaluation.
The evaluation relation is a binary relation on the set of terms.
Evaluation: t t‘