Problem 3
(*) Find the K’th element of a list. The first element in the list is number 1.
Example:
* (element-at '(a b c d e) 3) c
Example in Haskell:
Prelude> elementAt [1,2,3] 2 2 Prelude> elementAt "haskell" 5 'e'
(*) Find the K’th element of a list. The first element in the list is number 1.
Example:
* (element-at '(a b c d e) 3) c
Example in Haskell:
Prelude> elementAt [1,2,3] 2 2 Prelude> elementAt "haskell" 5 'e'
(*) Find the last but one element of a list.
(Note that the Lisp transcription of this problem is incorrect.)
Example in Haskell:
Prelude> myButLast [1,2,3,4] 3 Prelude> myButLast ['a'..'z'] 'y'
(*) Find the last element of a list.
(Note that the Lisp transcription of this problem is incorrect.)
Example in Haskell:
Prelude> myLast [1,2,3,4] 4 Prelude> myLast ['x','y','z'] 'z'
Solution:
The Untyped Lambda Calculus or the pure lambda calculus forms the computational substrate for most of the type systems.
Peter Landin observed that complex programming languages can be understood as having a tiny core with all the complex features implemented in the tiny core.
Lambda Calculus can be viewed as a simple programming language or as a mathematical object about which statements can be proved.
Everything is a function.
Definition 1 Lambda Term: It refers to any term in the lambda calculus.
Definition 2 Lambda Abstraction: Lambda terms beginning with a
are called lambda abstractions.
There are three kind of terms in the lambda calculus.
The grammar can be summarized as:
Syntax:
To save writing too many parenthesis the convention is that the
1. Scope
A variable is said to be bound when it occurs in the body {t} of an abstraction .
A variable is said to be free if it is not bound by enclosing abstraction on {x}
An abstraction with no free variables is said to be closed or a combinator.
2. Operational Semantics
In its pure form, lambda calculus has no mechanism for computation except function application, functions are applied to arguments which are themselves functions. Each step in computation is rewriting an application by replacing the value of the bound variable of the lambda abstraction with the argument given on the right side of the application.
There can be many different evaluation strategies.
3. Multiple Arguments
4. Church Booleans
5. Pairs
6. Church Numerals
A number n is encoded by the action of applying a function s to z n times.
7. Recursion
factorial = fix (lambda fct. body containing fct)
8. Formalities
Definition 3 The set of terms is the smallest set such that
- If
, then
.
- If elements
, then
.
- If
, then
.
Definition 4 The set of free variables of a term {t}, written as
is defined as the set


.
Definition 5 Substituiton:
Syntax:
Evaluation:
The following are present in this first language:
t = true
false
if t then t else t
0
succ t
prec t
iszero t
Programs
A program in the above language is a term built up from the forms given in the grammar.
if false then 0 else 1
1
1. Syntax
The grammar above is a way to specify the syntax of the language. One other way to do so is to specify it inductively using set theory.
Definition 1 Terms, Inductively: The set of terms is the smallest set
such that
- {true, false, 0}
.
- if
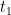
then succ(
), pred(
), iszero(
)
.
- if
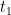
,
and
then if
then
else
.
Definition 2 Terms, By Inference Rules: The set of terms is defined by the following rules:
Rules set 1:
Rules set 2:
Rules set 3:
Each rule is read “If we have established the statements in the premise of the rules above, then the we may derive the conclusions in the lines below”. The rules with no premises are called axioms.
Definition 3 Terms, Concretely: The set of terms can also be given by constructing sets of successively bigger sizes.
For each natural number
we define a set
as follows:
Finally, let
Inference rules are just another way of writing the set theoretic definition.
Each inference rule may imply an infinite tree of terms.
Proposition 4
.
In definition on page we saw that a term can have one of three forms. This can be used in two ways:
The consts, size and depth functions can be defined using inductive definition over the set of terms. Relations between sizes and depths, the cardinality of consts and size can be proven using the definition of the set of terms.
2. Semantic Styles
2.1. Operational Semantics
The behaviour of the program is described by specifying an abstract machine for it.
The machine is abstract in the sense that the terms of the program are what form the machine code, instead of some low level language.
The terms are represented by states of an abstract machine. The meaning of a program is represented by the output of the computation of the abstract machine whose starting state is the first term of the program, that is the value in the final state.
It is customary to give two or more different operational semantics for a single language. One closer to the language in question and the other closer to the machine language.
Proving that the above two operational semantics correspond in some suitable sense amounts to proving that the implementation is correct.
2.2. Denotational Semantics
It takes a more abstract view of meaning and instead of defining the meaning of terms in terms of a sequence of machine states, the meaning of term is defined to be some mathematical object – a function or a number.
3. Evaluation
Consider a language with grammar as below:
Syntax:
Values, a subset of terms, are the possible final outcomes of evaluation.
The evaluation relation is a binary relation on the set of terms.
Evaluation: t t‘
Definition 5 Evaluation Strategy: The interplay between the rules determines a particular order of evaluation.
Definition 6 Computation Rules:
Definition 7 Congruence Rules:
Definition 8 An instance of an inference rule is obtained by replacing the metavariables in the premises and conclusions of the rule.
Definition 9 A rule is satisfied by a relation if each instance of the rule the conclusion is in the rule or one of the premises is not.
Definition 10 A one-step evaluation relation
is the smallest binary relation on the set of terms which satisfies all the evaluation inference rules for the set of terms.
Definition 11 When a pair (t, t’) is in the one-step evaluation relation we say that the evaluation statement t
t’ is derivable .
Theorem 12 (Determinacy of One-Step Evaluation) If t
t’ and t
t”, then t’
t”.
Definition 13 A term t is in normal form if no evaluation rule applies to it, i.e.\, if there is no t’ such that t
t’.
Theorem 14 Every value is in normal form.
Theorem 15 If t is in normal form, then t is a value.
Definition 16 The multi-step evaluation relation
is the reflexive, transitive closure of the one-step evaluation relation. If t
t’ and t’
t”, then t
t”.
Consider a language with grammar as below:
Syntax:
Values, a subset of terms, are the possible final outcomes of evaluation.
The evaluation relation is a binary relation on the set of terms.
Evaluation: t t‘
1. Sets, Relations and Functions
Definition 1 Countable Set: A set is countable if it can be placed in one-to-one correspondence with the set of natural numbers
.
Definition 2 n-place Relation: An n-place relation on a collection of sets
is a set
of tuples
. We say that elements
through
are related by
if
.
Definition 3 Predicates: A one place relation is also called a predicate. One-place relation on a set
is a subset
of
. It is written as
instead of
.
Definition 4 Binary Relation: A two place relation on sets
and
is also called a binary relation on the two sets. It is written as


instead of
.
Three or more place relations are written using the mixfix syntax. The elements are separated by symbols. For example, stands for the triple
.
Definition 5 Domain: The domain of a relation is the set of elements from the first set which are present in the tuples in the relation set.
Definition 6 Range: The domain of a relation is the set of elements from the first set which are present in the tuples in the relation set.
Definition 7 Partial Function: A binary relation
is a partial function if, whenever
and
, then, we have
.
Definition 8 Total Function: A partial function
is also a total function if the domain of R is the whole set.
Definition 9 A partial function
is said to be defined for an element
if
for some
. Otherwise, we write
or
to mean “
is undefined on
”.
2. Ordered Sets
Definition 10 Reflexive Relation: A binary relation
on
is said to be reflexive if
for all
.
Reflexiveness only makes sense for binary relations defined on a single set.
Definition 11 Symmetric Relation: A binary relation
on
is said to be symmetric if
for all
.
Definition 12 Transitive Relation: A binary relation
on
is said to be transitive if
for all
.
Definition 13 Anti-Symmetric Relation: A binary relation
on
is said to be anti-symmetric if
for all
.
Definition 14 Preorder: A reflexive and transitive relation on a set is called a preorder on that set. Preorders are usually written using symbols such as
or
.
Definition 15 Partial Order: A preorder which is also anti-symmetric is called a partial order.
Definition 16 Total Order: A partial order with the property that for every two elements
we have either
or
.
Definition 17 Join of two elements: It is the lowest upper bound for the set of elements which are greater than given two elements with respect to the partial order.
Definition 18 Meet of two elements: It is the greatest lower bound for the set of elements which are smaller than given two elements with respect to the partial order.
Definition 19 Equivalence Relation: A binary relation on a set is called an equivalence relation if it is reflexive, symmetric and transitive.
Definition 20 Reflexive Closure: A reflexive closure of a binary relation
on a set
is the smallest reflexive relation
which contains
. (Smallest in the sense that if some other reflexive relation
also contains
then
).
Definition 21 Transitive Closure: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
Definition 22 Sequence: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
Definition 23 Permutation: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
Definition 24 Decreasing Chain: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
Definition 25 Well Founded Preorder: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
3. Induction
Axiom (Principle of Ordinary Induction) Suppose that
is a predicate defined on natural numbers. Then:
If
and, for all
,
implies
,
then,
holds for all
.
1. Introduction
Hypothesis testing is a method of inference.
Definition 1 A hypothesis is a statement about a population parameter.
Definition 2 Null and Alternate Hypothesis: We partition the parameter space
into two disjoint sets
and
and we wish to test:
We call
the null hypothesis and
the alternate hypothesis.
Definition 3 Rejection Region: Let
be a random variable and let
be its range. Let
be the rejection region.
We accept
when
does not belong to
and reject when it does.
Hypothesis testing is a legal trial. We accept unless the evidence suggests otherwise. Falsely sentencing the accused when he is not guilty is type I error and letting the accused go free when he is infact guilty is a type II error.
Definition 4 Power Function of a Test: It is the probability of
being in the rejection region, expressed as a function of
.
Definition 5 Size of a Test: It is the maximum of the power function of a test when
is restricted to the
parameter space.
Definition 6 Level
Test: A test with size less than or equal to
is said to be a level
test.
Definition 7 Simple Hypothesis: A hypothesis of the form
is called a simple hypothesis.
Definition 8 Composite Hypothesis: A hypothesis of the form
or
is called a composite hypothesis.
Definition 9 Two Sided Test: A test of the form
is called a two-sided test.
Definition 10 One Sided Test: A test of the form
or
is called a one-sided test.
Example 1 (Hypothesis Testing on Normal Distribution:) Let
where
is known. We want to test
versus
. Hence
and
.
Consider the test:
where
.
Then the rejection region is
The power function of the test is
The size of the test is
Equating with
we obtain
Hence
We reject when
. For a test size of 95%
or we reject when
2. The Wald Test
Let be \textsc{iid} random variables with
as a parameter of their distribution function
. Let
be the estimate of
and let
be the standard deviation of the distribution of
.
Definition 11 (The Wald Test)
Consider testing a two-sided hypothesis:
Assume that
has an asymptotically normal distribution.
Then, the size
the Wald Test is: reject
if
where
Theorem 12 Asymptotically, the Wald test has size
.
Example 2 Two experiments are conducted to test two prediction algorithms.
The prediction algorithms are used to predict the outcomes
and
times, respectively, and have a probability of predicting with success as
and
, respectively.
Let
.
Consider testing a two-sided hypothesis:
3. The Likelihood Ratio Test
This test can be used to test vector valued parameters as well.
Definition 13 The likelihood ratio test statistic for testing
versus
is
There are two methods of estimating .
1. Method of Moments
It is a method of generating parametric estimators. These estimators are not optimal but they are easy to compute. They are also used to generate starting values for other numerical parametric estimation methods.
Definition 1 Moments and Sample Moments:
Suppose that the parameter
has
components:
. For
,
Define
moment as
Define
sample moment as
Definition 2
The method of moments estimator
is the value of
which satisfies
Why The Above Method Works: The method of moments estimator is obtained by equating the moment with the
sample moment. Since there are k of them we get k equations in k unknowns (the unknowns are the k parameters). This works because we can find out the
moments in terms of the unknown parameters and we can find the
sample moments numerically, since we know the sample values.
2. Maximum Likelihood Method
It is the most common method for estimating parameters in a parametric model.
Definition 3 Likelihood Function: Let
have a \textsc{pdf}
. The likelihood function is defined as
The log-likelihood fucntion is defined as
.
The likelihood function is the joint density of the data. We treat it as a function of the parameter . Thus
.
Definition 4 Maximum Likelihood Estimator: It is the value of
,
which maximizes the likelihood function.
Example 1 Let
be \textsc{iid} random variables with
distribution.
If
and
, then
. Otherwise
which is a decreasing function of
. Hence
.
3. Properties of MLE
4. Consistency of MLE
Definition 5 Kullback Leibler Distance:
Ifand
are \textsc{pdf}, the Kullback Leibler distance between them is defined as
5. Equivariance of MLE
6. Asymptotic Normality of MLE
The distribution of is asymptotically normal. We need the following definitions to prove it.
Definition 6 Score Function: Let
be a random variable with \textsc{pdf}
. Then the score function is defined as
Definition 7 Fisher Information: The Fisher Information is defined as
Theorem 8
Theorem 9
Theorem 10
Theorem 11
Definition 12 Let
.
Theorem 13
Theorem 14
Theorem 15 Let
.
In words, traps
with probability
. We call
the coverage of the confidence interval.
is random and
is fixed. Commonly, people use 95 percent confidence intervals, which corresponds to choosing
= 0.05. If
is a vector then we use a confidence set (such as a sphere or an ellipse) instead of an interval.
Theorem 16 (Normal Based Confidence Intervals)
Let
.
and let
be the \textsc{cdf} of a random variable
with standard normal distribution and
and let
Then,
For 95% confidence intervals is .95,
is .05,
is 1.96 and the interval is thus
.
1. Introduction
We assume that the data we are looking at comes from a probability distribution with some unknown parameters that control the exact shape of the distribution.
Definition 1 Statistical Inference: It is the process of using given data to infer the properties of the distribution (for example the values of the parameters) which generated the data. It is also called ‘learning’ in computer science.
Definition 2 Statistical Models: A statistical model is a set of distributions.
When we find out the form of the distribution (the equations that describe it) and the parameters used in the form we gain more understanding of the source of our data.
2. Parametric Models
Definition 3 Parametric Models: A parametric model is a statistical model which is parameterized by a finite number of parameters. A general form of a parametric model is
where
is an unknown parameter (or vector of parameters) that can take values in the parameter space
.
Example 1 An example of a parametric model is:
3. Non-Parametric Models
Definition 4 Non – Parametric Models: A non-parametric model is one in which
cannot be parameterized by a finite number of parameters.
3.1. Non-Paramateric Estimation of Functionals
Definition 5 Sobolev Space: Usually, it is not possible to estimate the probability distribution from the data by just assuming that it exists. We need to restrict the space of possible solutions. One way is to assume that the density function is a smooth function. The restricted space is called Sobolev Space.
Definition 6 Statistical Functional: Any function of \textsc{cdf}
is called a statistical functional.
Example 2 Statistical Functionals: The mean, variance and median can be thought of as functions of
:
The mean
is given as:
The variance is given as:
The median is given as:
4. Regression
Definition 7 Independent and Dependent Variables: We observe pairs of data:
.
is assumed to depend on
which is assumed to be the independent variable. The other names for these are, for:
: predictor, regressor, feature or independent variable.
: response variable, outcome or dependent variable.
Definition 8 Regression Function: The regression function is
Definition 9 Parametric and Non-Parametric Regression Models: If we assume that
is finite dimensional, then the model is a parametric regression model, otherwise it is a non-parametric regression model.
There can be three categories of regression, based on the purpose for which it was done:
Definition 10 Prediction: The goal of predicting
based on the value of
is called prediction.
Definition 11 Classification: If
is discrete then prediction is instead called classification.
Definition 12 Curve Estimation: If our goal is to estimate the function
, then we call this regression or curve estimation.
The regression function can be algebraically manipulated to express it in the form
where .
If is a parametric model, then we write
to denote the probability that X belongs to A. It does not mean that we are averaging over
, it means that the probability is calculated assuming the parameter is
.
5. Fundamental Concepts in Inference
Many inferential problems can be identified as being one of three types: estimation, confidence sets, or hypothesis testing.
5.1. Point Estimates
Definition 13 Point Estimation: Point estimation refers to providing a single “best guess” of some quantity of interest. The quantity of interest could be
- a parameter in a parametric model,
- a \textsc{cdf}
,
- a probability density function
,
- a regression function
, or
- a prediction for a future value
of some random variable.
By convention, we denote a point estimate of . Since
is a fixed, unknown quantity, the estimate
depends on the data so
is a random.
Definition 14 Point Estimator of
: Formally, let
be n \textsc{iid} data points from some distribution
. Then, a point estimator
of
is some function of
:
Definition 15 Bias of an Estimator: The bias of an estimator is defined as:
Definition 16 Consistent Estimator: A point estimator
of
is consistent if:
.
Definition 17 Sampling Distribution: The distribution of
is called sampling distribution.
Definition 18 Standard Error: The standard deviation of the sampling distribution is called standard error denoted by \textsf{se}.
In some cases, \textsf{se} depends upon the unkown distribution
. Its estimate is denoted by
.
Definition 19 Mean Squared Error: It is used to evaluate the quality of a point estimator. It is defined as
Example 3 Let
be \textsc{iid} random variables with Bernoulli distribution. Then
. Then,
. Hence,
is unbiased.
Definition 20 Asymptotically Normal Estimator: An estimator is asymptotically normal if
5.2. Confidence Sets
Definition 21 A
confidence interval for a parameter
is an interval
(where
and
are functions of the data), such that
In words, traps
with probability
. We call
the coverage of the confidence interval.
is random and
is fixed. Commonly, people use 95 percent confidence intervals, which corresponds to choosing
= 0.05. If
is a vector then we use a confidence set (such as a sphere or an ellipse) instead of an interval.
Theorem 22 (Normal Based Confidence Intervals)
Let
.
and let
be the \textsc{cdf} of a random variable
with standard normal distribution and
and let
Then,
For 95% confidence intervals is .95,
is .05,
is 1.96 and the interval is thus
.
5.3. Hypothesis Testing
In hypothesis testing, we start with some default theory – called a null hypothesis – and we ask if the data provide sufficient evidence to reject the theory. If not we retain the null hypothesis.
1. Introduction
There are two main ideas in this article.
2. Types of Convergence
Let be a sequence of random variables with distributions
and let
be a random variable with distribution
.
Definition 1 Convergence in Probability:
converges to
in probability, written as
, if for every
, we have
as
.
Definition 2 Convergence in Distribution:
converges to
in distribution, written as
, if
at all
for which
is continuous.
3. The Law of Large Numbers
Let be \textsc{iid} with mean
and variance
. Let sample mean be defined as
. It can be shown that
and
.
Theorem 3 Weak Law of Large Numbers: If
are \textsc{iid} random variables, then
.
4. The Central Limit Theorem
The law of large numbers says that the distribution of the sample mean, , piles up near the true distribution mean,
. The central limit theorem further adds that the distribution of the sample mean approaches a Normal distribution as n gets large. It even gives the mean and the variance of the normal distribution.
Theorem 4 The Central Limit Theorem: Let
be \textsc{iid} random variables with mean
and standard deviation
. Let sample mean be defined as
. Then the asymptotic behaviour of the distribution of the sample mean is given by
The other ways of expressing the above equation are
Definition 5 As has been defined in the Expectation chapter, if
are random variables, then we define the sample variance as
Theorem 6 Assuming the conditions of the CLT,
5. The Delta Method
Theorem 7 Let
be a random variable with conditions of CLT met, and let
be a differentiable function with
. Then,