Problem 1
(*) Find the last element of a list.
(Note that the Lisp transcription of this problem is incorrect.)
Example in Haskell:
Prelude> myLast [1,2,3,4] 4 Prelude> myLast ['x','y','z'] 'z'
Solution:
(*) Find the last element of a list.
(Note that the Lisp transcription of this problem is incorrect.)
Example in Haskell:
Prelude> myLast [1,2,3,4] 4 Prelude> myLast ['x','y','z'] 'z'
Solution:
The Untyped Lambda Calculus or the pure lambda calculus forms the computational substrate for most of the type systems.
Peter Landin observed that complex programming languages can be understood as having a tiny core with all the complex features implemented in the tiny core.
Lambda Calculus can be viewed as a simple programming language or as a mathematical object about which statements can be proved.
Everything is a function.
Definition 1 Lambda Term: It refers to any term in the lambda calculus.
Definition 2 Lambda Abstraction: Lambda terms beginning with a
are called lambda abstractions.
There are three kind of terms in the lambda calculus.
The grammar can be summarized as:
Syntax:
To save writing too many parenthesis the convention is that the
1. Scope
A variable is said to be bound when it occurs in the body {t} of an abstraction .
A variable is said to be free if it is not bound by enclosing abstraction on {x}
An abstraction with no free variables is said to be closed or a combinator.
2. Operational Semantics
In its pure form, lambda calculus has no mechanism for computation except function application, functions are applied to arguments which are themselves functions. Each step in computation is rewriting an application by replacing the value of the bound variable of the lambda abstraction with the argument given on the right side of the application.
There can be many different evaluation strategies.
3. Multiple Arguments
4. Church Booleans
5. Pairs
6. Church Numerals
A number n is encoded by the action of applying a function s to z n times.
7. Recursion
factorial = fix (lambda fct. body containing fct)
8. Formalities
Definition 3 The set of terms is the smallest set such that
- If
, then
.
- If elements
, then
.
- If
, then
.
Definition 4 The set of free variables of a term {t}, written as
is defined as the set


.
Definition 5 Substituiton:
Syntax:
Evaluation:
The following are present in this first language:
t = true
false
if t then t else t
0
succ t
prec t
iszero t
Programs
A program in the above language is a term built up from the forms given in the grammar.
if false then 0 else 1
1
1. Syntax
The grammar above is a way to specify the syntax of the language. One other way to do so is to specify it inductively using set theory.
Definition 1 Terms, Inductively: The set of terms is the smallest set
such that
- {true, false, 0}
.
- if
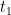
then succ(
), pred(
), iszero(
)
.
- if
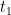
,
and
then if
then
else
.
Definition 2 Terms, By Inference Rules: The set of terms is defined by the following rules:
Rules set 1:
Rules set 2:
Rules set 3:
Each rule is read “If we have established the statements in the premise of the rules above, then the we may derive the conclusions in the lines below”. The rules with no premises are called axioms.
Definition 3 Terms, Concretely: The set of terms can also be given by constructing sets of successively bigger sizes.
For each natural number
we define a set
as follows:
Finally, let
Inference rules are just another way of writing the set theoretic definition.
Each inference rule may imply an infinite tree of terms.
Proposition 4
.
In definition on page we saw that a term can have one of three forms. This can be used in two ways:
The consts, size and depth functions can be defined using inductive definition over the set of terms. Relations between sizes and depths, the cardinality of consts and size can be proven using the definition of the set of terms.
2. Semantic Styles
2.1. Operational Semantics
The behaviour of the program is described by specifying an abstract machine for it.
The machine is abstract in the sense that the terms of the program are what form the machine code, instead of some low level language.
The terms are represented by states of an abstract machine. The meaning of a program is represented by the output of the computation of the abstract machine whose starting state is the first term of the program, that is the value in the final state.
It is customary to give two or more different operational semantics for a single language. One closer to the language in question and the other closer to the machine language.
Proving that the above two operational semantics correspond in some suitable sense amounts to proving that the implementation is correct.
2.2. Denotational Semantics
It takes a more abstract view of meaning and instead of defining the meaning of terms in terms of a sequence of machine states, the meaning of term is defined to be some mathematical object – a function or a number.
3. Evaluation
Consider a language with grammar as below:
Syntax:
Values, a subset of terms, are the possible final outcomes of evaluation.
The evaluation relation is a binary relation on the set of terms.
Evaluation: t t‘
Definition 5 Evaluation Strategy: The interplay between the rules determines a particular order of evaluation.
Definition 6 Computation Rules:
Definition 7 Congruence Rules:
Definition 8 An instance of an inference rule is obtained by replacing the metavariables in the premises and conclusions of the rule.
Definition 9 A rule is satisfied by a relation if each instance of the rule the conclusion is in the rule or one of the premises is not.
Definition 10 A one-step evaluation relation
is the smallest binary relation on the set of terms which satisfies all the evaluation inference rules for the set of terms.
Definition 11 When a pair (t, t’) is in the one-step evaluation relation we say that the evaluation statement t
t’ is derivable .
Theorem 12 (Determinacy of One-Step Evaluation) If t
t’ and t
t”, then t’
t”.
Definition 13 A term t is in normal form if no evaluation rule applies to it, i.e.\, if there is no t’ such that t
t’.
Theorem 14 Every value is in normal form.
Theorem 15 If t is in normal form, then t is a value.
Definition 16 The multi-step evaluation relation
is the reflexive, transitive closure of the one-step evaluation relation. If t
t’ and t’
t”, then t
t”.
Consider a language with grammar as below:
Syntax:
Values, a subset of terms, are the possible final outcomes of evaluation.
The evaluation relation is a binary relation on the set of terms.
Evaluation: t t‘
1. Sets, Relations and Functions
Definition 1 Countable Set: A set is countable if it can be placed in one-to-one correspondence with the set of natural numbers
.
Definition 2 n-place Relation: An n-place relation on a collection of sets
is a set
of tuples
. We say that elements
through
are related by
if
.
Definition 3 Predicates: A one place relation is also called a predicate. One-place relation on a set
is a subset
of
. It is written as
instead of
.
Definition 4 Binary Relation: A two place relation on sets
and
is also called a binary relation on the two sets. It is written as


instead of
.
Three or more place relations are written using the mixfix syntax. The elements are separated by symbols. For example, stands for the triple
.
Definition 5 Domain: The domain of a relation is the set of elements from the first set which are present in the tuples in the relation set.
Definition 6 Range: The domain of a relation is the set of elements from the first set which are present in the tuples in the relation set.
Definition 7 Partial Function: A binary relation
is a partial function if, whenever
and
, then, we have
.
Definition 8 Total Function: A partial function
is also a total function if the domain of R is the whole set.
Definition 9 A partial function
is said to be defined for an element
if
for some
. Otherwise, we write
or
to mean “
is undefined on
”.
2. Ordered Sets
Definition 10 Reflexive Relation: A binary relation
on
is said to be reflexive if
for all
.
Reflexiveness only makes sense for binary relations defined on a single set.
Definition 11 Symmetric Relation: A binary relation
on
is said to be symmetric if
for all
.
Definition 12 Transitive Relation: A binary relation
on
is said to be transitive if
for all
.
Definition 13 Anti-Symmetric Relation: A binary relation
on
is said to be anti-symmetric if
for all
.
Definition 14 Preorder: A reflexive and transitive relation on a set is called a preorder on that set. Preorders are usually written using symbols such as
or
.
Definition 15 Partial Order: A preorder which is also anti-symmetric is called a partial order.
Definition 16 Total Order: A partial order with the property that for every two elements
we have either
or
.
Definition 17 Join of two elements: It is the lowest upper bound for the set of elements which are greater than given two elements with respect to the partial order.
Definition 18 Meet of two elements: It is the greatest lower bound for the set of elements which are smaller than given two elements with respect to the partial order.
Definition 19 Equivalence Relation: A binary relation on a set is called an equivalence relation if it is reflexive, symmetric and transitive.
Definition 20 Reflexive Closure: A reflexive closure of a binary relation
on a set
is the smallest reflexive relation
which contains
. (Smallest in the sense that if some other reflexive relation
also contains
then
).
Definition 21 Transitive Closure: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
Definition 22 Sequence: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
Definition 23 Permutation: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
Definition 24 Decreasing Chain: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
Definition 25 Well Founded Preorder: A transitive closure of a binary relation
on a set
is the smallest transitive relation
which contains
. (Smallest in the sense that if some other transitive relation
also contains
then
). It is written as
.
3. Induction
Axiom (Principle of Ordinary Induction) Suppose that
is a predicate defined on natural numbers. Then:
If
and, for all
,
implies
,
then,
holds for all
.
Exercise 3.23. A deque (“double-ended queue”) is a sequence in which items can be inserted and deleted at either the front or the rear. Operations on deques are the constructor make-deque, the predicate empty-deque?, selectors front-deque and rear-deque, and mutators front-insert-deque!, rear-insert-deque!, front-delete-deque!, and rear-delete-deque!. Show how to represent deques using pairs, and give implementations of the operations.23 All operations should be accomplished in  (1) steps.
(1) steps.
Exercise 3.50. Complete the following definition, which generalizes stream-map to allow procedures that take multiple arguments, analogous to map in section 2.2.3, footnote 12.
(define (stream-map proc . argstreams)
(if (<??> (car argstreams))
the-empty-stream
(<??>
(apply proc (map <??> argstreams))
(apply stream-map
(cons proc (map <??> argstreams))))))
Exercise 3.35. Ben Bitdiddle tells Louis that one way to avoid the trouble in exercise 3.34 is to define a squarer as a new primitive constraint. Fill in the missing portions in Ben’s outline for a procedure to implement such a constraint:
(define (squarer a b)
(define (process-new-value)
(if (has-value? b)
(if (< (get-value b) 0)
(error "square less than 0 -- SQUARER" (get-value b))
<alternative1>)
<alternative2>))
(define (process-forget-value) <body1>)
(define (me request) <body2>)
<rest of definition>
me)
Exercise 3.34. Louis Reasoner wants to build a squarer, a constraint device with two terminals such that the value of connector b on the second terminal will always be the square of the value a on the first terminal. He proposes the following simple device made from a multiplier:
(define (squarer a b)
(multiplier a a b))
There is a serious flaw in this idea. Explain.