Analysis – Gaurav Sharma's Blog

If you are not familiar with function spaces, please read Function Spaces post before reading this.

Sines and cosines form an orthonormal basis for the function space.

If we want to use other functions as basis, we encounter the problem of their not being orthogonal to each other. For example, if we choose the simplest functions, the powers of x as a basis, then we cannot find any interval on which 1 and ${x^2}$ are orthogonal to each other.

Not being orthogonal makes it hard to find projections or coefficients of the decomposition. The computational effort increases as the number of functions is increased.

However, this problem can be solved if we can create other orthonormal basis for function space by using Gram Schmidt orthogonalization over any set of independent functions.

Legendre polynomials are obtained by this orthogonalization carried while starting with powers of ${x}$ as the initial basis.

We chose the interval ${-1 \leq x \leq 1}$ so as to make even powers of ${x}$ orthogonal to the odd powers of ${x}$ . Thus 1 and ${x}$ become orthogonal.

We need to orthogonalize ${x^2}$ with respect to 1 and ${x}$ .

Thus the third orthogonal polynomials is

$\displaystyle v_3 = x^2 - \frac{(1, x^2)}{(1,1)}1 - \frac{(x, x^2)}{(x,x)}x = x^2 - \frac{\int_{-1}^1x^2dx}{\int_{-1}^11dx} = x^2 - \frac{1}{3}.\ \ \ \ \ (1)$

The polynomials thus constructed by carrying out this process are called Legendre polynomials and they are orthogonal to each other over the interval ${-1 \leq x \leq 1}$ .

The first few Legendre polynomials are:

0: ${ 1}$

1: ${ x }$

2: ${ \frac12 (3x^2-1) }$

3: ${ \frac12 (5x^3-3x) }$

4: ${ \frac18 (35x^4-30x^2+3) }$

5: ${ \frac18 (63x^5-70x^3+15x) }$

6: ${ \frac1{16} (231x^6-315x^4+105x^2-5) }$

7: ${ \frac1{16} (429x^7-693x^5+315x^3-35x) }$

8: ${ \frac1{128} (6435x^8-12012x^6+6930x^4-1260x^2+35) }$

9: ${ \frac 1 {128} (12155x^9-25740x^7+18018x^5-4620x^3+315x) }$

10: ${ \frac1{256} (46189x^{10}-109395x^8+90090x^6-30030x^4+3465x^2-63)}$

A more complicated definition of these polynomials is that they are the solution to the following differential equation (Legendre’s differential equation):

$\displaystyle {d \over dx} \left[ (1-x^2) {d \over dx} P_n(x) \right] + n(n+1)P_n(x) = 0.\ \ \ \ \ (2)$

The solution is given by Rodrigues’ formula:

$\displaystyle P_n(x) = {1 \over 2^n n!} {d^n \over dx^n } \left[ (x^2 -1)^n \right].\ \ \ \ \ (3)$

We started with natural numbers to count discrete objects. Then we extended them to integers to have the closure property satisfied for the subtraction operator (or less formally, to be able to use numbers to describe profit and loss statements).

Then we extended them to rationals to talk about ratios, then to reals to include square and other roots and sums of infinite series (transcendental numbers). Then we extended them to complex numbers to have the closure property satisfied for the square roots and thus to exponentiation by rationals.

We also extend it to vectors, numbers that have two, three or n dimentions and to Hamiltonions (quaternions) which are a generalization of complex numbers etc.

This extension of the concept of numbers is driven partially by the need to model the world efficiently, many of the extensions have come from physics.

When we look back at the new theories that resulted while extending the concept of numbers of we can extract out common patterns in the number systems and their spaces and this gives rise to mathematical structures such as groups, rings, fields etc.

Function spaces is essentially extending the concept of numbers to include functions.

To understand function spaces, we first need to understand Hilbert space. To create a Hilbert space, we start with ${R^n}$ and extend it to ${R^{\infty}}$ .

Thus our space contains vectors with an infinite sequence of components. The length of vectors in this space can be defined analogously to the way it is defined in ${R^n}$ , that is by sums of squares of the individual components with ${n \rightarrow \infty}$ .

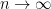Length squared:

$\displaystyle \lVert v \rVert^2 = v_1^2 + {v_2}^2 + \dots \ \ \ \ \ (1)$

Inner products and orthogonality are defined just be letting 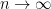${n \rightarrow \infty}$ in the ${R^n}$ definitions of these quantities.

$\displaystyle v^Tw = v_1w_1 + v_2w_2 + v_3w_3 + \dots \ \ \ \ \ (2)$

Now we are ready to extend Hilbert space to a function space. Since function space includes continuous functions on the real line, the number of values is uncountably infinite and cannot be listed. So instead of summing the square of components we use the integral of the square of the function over some interval as our definition of length of the vector which is here a continuous function.

Length definition for function space:

$\displaystyle \lVert f \rVert^2 = \int_0^{2 \pi}(f(x))^2 dx \ \ \ \ \ (3)$

We can use the same idea of replacing infinite summation by integration to define inner products of two vectors, or here as we are in a function space, to two functions.

$\displaystyle (f, g) = \int_0^{2 \pi}f(x)g(x) dx \ \ \ \ \ (4)$

Sines and cosines, that is ${sin \thinspace nx}$ and ${cos \thinspace nx}$ , form an orthonormal basis for this space (after dividing by their length which is ${\sqrt{\pi}}$ ).

$\displaystyle \lVert sin \thinspace x \rVert^2 = \int_0^{2 \pi}(sin \thinspace x)^2 dx = \pi \ \ \ \ \ (5)$

and

$\displaystyle (sin, cos) = \int_0^{2 \pi}sin \thinspace x \thinspace cos \thinspace x \thinspace dx = 0 \ \ \ \ \ (6)$

Just as we can write any vector as a linear combination of the basis vectors for a space, we can write any function as a linear combination of the sines and cosines.

This decomposition of a function into a series of sines and cosines is called the Fourier Series of that function.

$\displaystyle f(x) = a_0 + a_1cos \thinspace x + b_1sin \thinspace x + a_2cos \thinspace 2x + b_2sin \thinspace 2x + \dots \ \ \ \ \ (7)$

The coefficients ${a_is}$ and ${b_is}$ can be calculated in the same way we calculate them in finite dimensional vector spaces. We multiply both sides by a basis vector. All term but one on the right hand side then become zero (due to orthogonality of the basis vectors). Thus the coefficients can be calculated in terms of the norms and the inner products of the basis vectors with the given vector that is to be written as a linear combination.

As an example, to find ${b_1}$ , we multiply both sides by the corresponding function ${sin \thinspace x}$ and integrate over the interval 0 to ${2\pi}$ .

$\displaystyle \int_0^{2 \pi}f(x)sin \thinspace x \thinspace dx = a_0\int_0^{2 \pi}sin \thinspace x \thinspace dx + a_1 \int_0^{2 \pi}cos \thinspace x \thinspace sin \thinspace x \thinspace dx + b_1\int_0^{2 \pi}(sin \thinspace x)^2 dx + \dots \ \ \ \ \ (8)$

As has already been mentioned, all integrals on the right hand side except the one in which sin multiplies itself are zero. Thus ${b_1}$ is:

$\displaystyle b_1 = \frac{\int_0^{2 \pi}f(x)sin \thinspace x \thinspace dx}{\int_0^{2 \pi}(sin \thinspace x)^2 dx} \ \ \ \ \ (9)$

To see the analogy with projections, 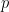${p}$ , the component of vector 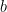${b}$ , along the line spanned by ${a}$ is

$\displaystyle p = \frac{b^Ta}{a^Ta} \ \ \ \ \ (10)$

It is helpful to see equation 9 as analogous to equation 10 for function spaces.

Here we are projecting the vector 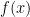${f(x)}$ onto ${sin \thinspace x}$ vector (they are ofcourse not truly vectors, but it is easier to see the analogy if they are thought of as vectors).

Category: Analysis

Legendre Polynomials – Gram Schmidt for Function Spaces

Function Spaces and Fourier Series