1. Introduction
Definition 1
Random Variable: A random variable  is a mapping
is a mapping

which assigns real numbers  to outcomes
to outcomes 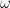 in
in  .
.
2. Distribution Functions
Definition 2
Distribution Function: Given a random variable  , the cumulative distribution function (also called the \textsc{cdf}) is a function
, the cumulative distribution function (also called the \textsc{cdf}) is a function ![{F_X \colon \mathbb{R} \rightarrow [0,1]} {F_X \colon \mathbb{R} \rightarrow [0,1]}](http://s0.wp.com/latex.php?latex=%7BF_X+%5Ccolon+%5Cmathbb%7BR%7D+%5Crightarrow+%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0) defined by:
defined by:

Theorem 3 Let  have \textsc{cdf}
have \textsc{cdf} 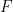 and let
and let 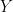 have \textsc{cdf}
have \textsc{cdf}  . If
. If  for all
for all  then
then  for all
for all 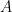 .
.
Definition 4  is discrete if it takes countably many infinite values.
is discrete if it takes countably many infinite values.
We define the probability function or the probability mass function for  by
by  .
.
Definition 5 A random variable  is said to be continuous if there exists a function
is said to be continuous if there exists a function  such that
such that
 for all
for all  ,
,
 for all
for all  with
with  we have
we have

The function  is called the probability density function and we have
is called the probability density function and we have

and  at all points for which
at all points for which  is differentiable.
is differentiable.
3. Important Discrete Random Variables
Remark 1 We write  to denote that the random variable
to denote that the random variable  has a \textsc{cdf}
has a \textsc{cdf} 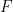 .
.
3.1. The Point Mass Distribution
\textsc{The Point Mass Distribution}. X has a point mass distribution at  , written
, written  if
if  . Hence
. Hence  is
is

3.2. The Discrete Uniform Distribution
\textsc{The Discrete Uniform Distribution}. Let  be a given integer. Let
be a given integer. Let  have a probability mass function given by:
have a probability mass function given by:

Then  has a discrete uniform distribution on
has a discrete uniform distribution on  .
.
3.3. The Bernoulli Distribution
\textsc{The Bernoulli Distribution}. Let  be a random variable with
be a random variable with  and
and  for some
for some ![{p \in [0, 1]} {p \in [0, 1]}](http://s0.wp.com/latex.php?latex=%7Bp+%5Cin+%5B0%2C+1%5D%7D&bg=ffffff&fg=000000&s=0) . We say that
. We say that  has a Bernoulli Distribution written as
has a Bernoulli Distribution written as  . The probability function
. The probability function  is given by
is given by  .
.
3.4. The Binomial Distribution
\textsc{The Binomial Distribution}. Flip a coin 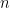 times and let
times and let  denote the number of heads. If
denote the number of heads. If  denotes the probability of getting heads in a single coin toss and the tosses are assumed to be independent then the \textsc{pdf} of
denotes the probability of getting heads in a single coin toss and the tosses are assumed to be independent then the \textsc{pdf} of  can be shown to be:
can be shown to be:

3.5. The Geometric Distribution
\textsc{The Geometric Distribution}.  has a geometric distribution with parameter
has a geometric distribution with parameter ![{p \in [0, 1]} {p \in [0, 1]}](http://s0.wp.com/latex.php?latex=%7Bp+%5Cin+%5B0%2C+1%5D%7D&bg=ffffff&fg=000000&s=0) , written as
, written as  if
if

 is the number of flips needed until the first head appears.
is the number of flips needed until the first head appears.
3.6. The Poisson Distribution
\textsc{The Poisson Distribution}.  has a Poisson distribution with parameter
has a Poisson distribution with parameter 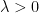 , written as
, written as  if
if

 is the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since the last event.
is the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since the last event.
4. Important Continuous Random Variables
4.1. The Uniform Distribution
\textsc{The Uniform Distribution}. For  , X has a uniform distribution over
, X has a uniform distribution over  , written
, written  , if
, if
![\displaystyle f_X(x) = \begin{cases} \frac{1}{b - a} & x \in [a, b] \\ 0 & \text{otherwise}. \end{cases} \ \ \ \ \ (10) \displaystyle f_X(x) = \begin{cases} \frac{1}{b - a} & x \in [a, b] \\ 0 & \text{otherwise}. \end{cases} \ \ \ \ \ (10)](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle++f_X%28x%29+%3D+%5Cbegin%7Bcases%7D+%5Cfrac%7B1%7D%7Bb+-+a%7D+%26+x+%5Cin+%5Ba%2C+b%5D+%5C%5C+0+%26+%5Ctext%7Botherwise%7D.+%5Cend%7Bcases%7D+%5C+%5C+%5C+%5C+%5C+%2810%29&bg=ffffff&fg=000000&s=0)
4.2. The Normal Distribution
\textsc{The Normal Distribution}. We say that  has a normal (or Gaussian) distribution with parameters
has a normal (or Gaussian) distribution with parameters 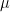 and
and 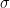 , written as
, written as  if
if

The parameter 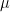 is the “center” (or mean) of the distribution and
is the “center” (or mean) of the distribution and 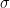 is the “spread” (or standard deviation) of the distribution. We say that
is the “spread” (or standard deviation) of the distribution. We say that  has a standard Normal distribution if
has a standard Normal distribution if  and
and  . A standard Normal random variable is denoted by
. A standard Normal random variable is denoted by  . The \textsc{pdf} and \textsc{cdf} of a standard Normal are denoted by
. The \textsc{pdf} and \textsc{cdf} of a standard Normal are denoted by  and
and  . The \textsc{pdf} is plotted in Figure There is no closed-form expression for
. The \textsc{pdf} is plotted in Figure There is no closed-form expression for 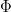 . Here are some useful facts:
. Here are some useful facts:
If  , then
, then  .
If
.
If  , then
, then  .
If
.
If  for
for  are independent, then we have
are independent, then we have

It follows from  that if
that if 




Example 1 Suppose that  . Find
. Find  .
.
Solution:

Example 2 For the above problem, also find the value  of
of  such that
such that  . Solution:
. Solution:

From the normal table, we have that 

4.3. The Exponential Distribution
\textsc{The Exponential Distribution}.  has an exponential distribution with parameter
has an exponential distribution with parameter  , written as
, written as  , if
, if

4.4. The Gamma Distribution
\textsc{The Gamma Distribution}. For  , the Gamma function is defined as
, the Gamma function is defined as

 has a Gamma distribution with parameters
has a Gamma distribution with parameters 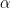 and
and 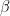 (where
(where  ), written as
), written as  , if
, if

 is the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since the last event.
is the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since the last event.
5. Bivariate Distributions
Definition 6 Given a pair of discrete random variables  and
and 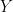 , their joint mass function is defined as
, their joint mass function is defined as 
Definition 7 For two continuous random variables,  and
and 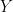 , we call a function
, we call a function  a \textsc{pdf} of random variables
a \textsc{pdf} of random variables  if
if
 for all
for all  ,
,
 For any set
For any set  we have
we have

Example 3 For  , let
, let  have density
have density

Find the value of  .
.
Solution: We equate the integral of 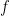 over
over  to
to 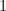 and find
and find  .
.

6. Marginal Distributions
Definition 8 For the discrete case, if  have a joint mass distribution
have a joint mass distribution  then the marginal distribution of
then the marginal distribution of  is given by
is given by

and of 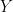 is given by
is given by

Definition 9 For the continuous case, if  have a probability distribution function
have a probability distribution function  then the marginal distribution of
then the marginal distribution of  is given by
is given by

and of 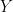 is given by
is given by

7. Independent Random Variables
Definition 10 Two random variables,  and
and 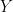 are said to be independent if for every
are said to be independent if for every 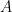 and
and 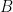 we have
we have

Theorem 11 Let  and
and 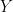 have a joint \textsc{pdf}
have a joint \textsc{pdf}  . Then
. Then  if
if  for all values of
for all values of  and
and 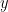 .
.
8. Conditional Distributions
Definition 12 Let  and
and 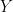 have a joint \textsc{pdf}
have a joint \textsc{pdf}  . Then the conditional distribution of
. Then the conditional distribution of  given Y is defined as
given Y is defined as

9. Multivariate Distributions and \textsc
Samples}
Definition 13 Independence of 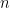 random variables: Let
random variables: Let  where
where  are random variables. Let
are random variables. Let  denote their \textsc{pdf}. We say that
denote their \textsc{pdf}. We say that  are independent if for every
are independent if for every  ,
,

Definition 14 If  are independent random variables with the same marginal distribution
are independent random variables with the same marginal distribution 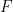 , we say that
, we say that  are \textsc{iid} (identically and independently distributed) random variables and we write:
are \textsc{iid} (identically and independently distributed) random variables and we write:

If 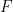 has density
has density 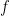 then we also write
then we also write  . We also call
. We also call  a random sample of size
a random sample of size 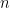 from
from 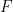 .
.
10. The Multivariate Normal Distribution
\textsc{The Multivariate Normal Distribution} In the multivariate normal distribution, the parameter 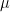 is a vector and the parameter
is a vector and the parameter 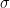 is a matrix
is a matrix  . Let
. Let

where  are independent. The joint density of
are independent. The joint density of  is
is

be a sequence of random variables with distributions
and let
be a random variable with distribution
.
converges to
in probability, written as
, if for every
, we have
.
converges to
in distribution, written as
, if
for which
is continuous.
be \textsc{iid} with mean
and variance
. Let sample mean be defined as
. It can be shown that
and
.
are \textsc{iid} random variables, then
.
, piles up near the true distribution mean,
. The central limit theorem further adds that the distribution of the sample mean approaches a Normal distribution as n gets large. It even gives the mean and the variance of the normal distribution.
be \textsc{iid} random variables with mean
and standard deviation
. Let sample mean be defined as
. Then the asymptotic behaviour of the distribution of the sample mean is given by
are random variables, then we define the sample variance as
be a random variable with conditions of CLT met, and let
be a differentiable function with
. Then,