Suppose that a scalar 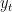 is related to a
is related to a  vector,
vector,  and a disturbance term
and a disturbance term  according to the regression model.
according to the regression model.

In this article, we will study the estimation and hypothesis testing of 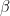 when
when  is deterministic and
is deterministic and  is i.i.d. Gaussian.
is i.i.d. Gaussian.
1. The Algebra of Linear Regression
Given a sample of T values of 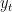 and the vector
and the vector  , the ordinary least squares (OLS) estimate of
, the ordinary least squares (OLS) estimate of 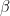 , denoted as
, denoted as 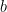 , is the value of
, is the value of 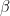 which minimizes the residual sum of squares (RSS).
which minimizes the residual sum of squares (RSS).

The OLS estimate of 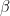 , b, is given by:
, b, is given by:

The model is written in matrix notation as:


where 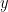 is a
is a  vector,
vector, 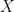 is a
is a  matrix,
matrix, 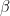 is a
is a  vector and
vector and  is a
is a  vector.
vector.
Thus,

Similarly,
![\displaystyle \hat u = y - Xb = y - X(X^TX)^{-1}X^Ty = [I_T - X(X^TX)^{-1}X^T]y = M_Xy. \ \ \ \ \ (7) \displaystyle \hat u = y - Xb = y - X(X^TX)^{-1}X^Ty = [I_T - X(X^TX)^{-1}X^T]y = M_Xy. \ \ \ \ \ (7)](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Chat+u+%3D+y+-+Xb+%3D+y+-+X%28X%5ETX%29%5E%7B-1%7DX%5ETy+%3D+%5BI_T+-+X%28X%5ETX%29%5E%7B-1%7DX%5ET%5Dy+%3D+M_Xy.+%5C+%5C+%5C+%5C+%5C+%287%29&bg=ffffff&fg=000000&s=0)
where  is defined as:
is defined as:
![\displaystyle M_X = [I_T - X(X^TX)^{-1}X^T]. \ \ \ \ \ (8) \displaystyle M_X = [I_T - X(X^TX)^{-1}X^T]. \ \ \ \ \ (8)](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+M_X+%3D+%5BI_T+-+X%28X%5ETX%29%5E%7B-1%7DX%5ET%5D.+%5C+%5C+%5C+%5C+%5C+%288%29&bg=ffffff&fg=000000&s=0)
 is a projection matrix. Hence it is symmetric and idempotent.
is a projection matrix. Hence it is symmetric and idempotent.


Since  is the projection matrix for the space orthogonal to
is the projection matrix for the space orthogonal to 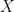 ,
,

Thus, we can verify that the sample residuals are orthogonal to 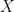 .
.

The sample residual is constructed from the sample estimate of 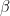 which is
which is 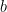 . The population residual is a hypothetical construct based on the true population value of
. The population residual is a hypothetical construct based on the true population value of 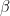 .
.


![\displaystyle \hat u = y - Xb = [I_T - X(X^TX)^{-1}X^T]y = M_Xy = M_XX b + u. \ \ \ \ \ (15) \displaystyle \hat u = y - Xb = [I_T - X(X^TX)^{-1}X^T]y = M_Xy = M_XX b + u. \ \ \ \ \ (15)](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Chat+u+%3D+y+-+Xb+%3D+%5BI_T+-+X%28X%5ETX%29%5E%7B-1%7DX%5ET%5Dy+%3D+M_Xy+%3D+M_XX+b+%2B+u.+%5C+%5C+%5C+%5C+%5C+%2815%29&bg=ffffff&fg=000000&s=0)

The fit of OLS is described in terms of  , which is defined as the ratio of squares of the fitted values (
, which is defined as the ratio of squares of the fitted values ( to the observed values of
to the observed values of 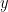 .
.

2. Assumptions on X and u
We shall assume that
(a) X will be deterministic
(b)  is i.i.d with mean 0 and variance
is i.i.d with mean 0 and variance  .
.
(c)  is Gaussian.
is Gaussian.
2.1. Properties of Estimated b Under Above Assumptions
Since,

Taking expectations of both sides, we have,

And the variance covariance matrix is given by,
![\displaystyle \mathop{\mathbb E}[(b - \beta)(b - \beta)^T] = \mathop{\mathbb E}[((X^TX)^{-1}X^Tu)((X^TX)^{-1}X^Tu)^T] = \sigma^2(X^TX)^{-1}. \ \ \ \ \ (20) \displaystyle \mathop{\mathbb E}[(b - \beta)(b - \beta)^T] = \mathop{\mathbb E}[((X^TX)^{-1}X^Tu)((X^TX)^{-1}X^Tu)^T] = \sigma^2(X^TX)^{-1}. \ \ \ \ \ (20)](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cmathop%7B%5Cmathbb+E%7D%5B%28b+-+%5Cbeta%29%28b+-+%5Cbeta%29%5ET%5D+%3D+%5Cmathop%7B%5Cmathbb+E%7D%5B%28%28X%5ETX%29%5E%7B-1%7DX%5ETu%29%28%28X%5ETX%29%5E%7B-1%7DX%5ETu%29%5ET%5D+%3D+%5Csigma%5E2%28X%5ETX%29%5E%7B-1%7D.+%5C+%5C+%5C+%5C+%5C+%2820%29&bg=ffffff&fg=000000&s=0)
Thus b is unbiased and is a linear function of y.
2.2. Distribution of Estimated b Under Above Assumptions
As u is Gaussian,

implies that b is also Gaussian.

2.3. Properties of Estimated Sample Variance Under Above Assumptions
The OLS estimate of variance of u,  is given by:
is given by:

Since  is a projection matrix and is symmetric and idempotent, it can be written as:
is a projection matrix and is symmetric and idempotent, it can be written as:

where

and 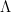 is a diagonal matrix with eigenvalues of
is a diagonal matrix with eigenvalues of  on the diagonal.
on the diagonal.
Since,

that is, since the two spaces that they represent are orthogonal to each other, it follows that:

whenever v is a column of X. Since we assume X to be of full rank, there are k such vectors and their eigenvalue is the right hand side, which is 0.
Also since

Thus, it follows that

whenever v is orthogonal to X. Since there are (T – k) such vectors,  has (T – k) eigenvectors with eigenvalue 1.
has (T – k) eigenvectors with eigenvalue 1.
Thus 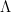 has k zeroes and (T – k) 1s on the diagonal.
has k zeroes and (T – k) 1s on the diagonal.

Let

Then,


As these  s are all unity, we have:
s are all unity, we have:

Also,

Thus, elements of w are uncorrelated with each other, have mean 0 and variance  .
.
Since each w has expectation of  ,
,

Hence,

2.4. Distribution of Estimated Sample Variance Under Above Assumptions
Since

when u is Gaussian, w is also Gaussian.
Then,

implies that  is the sum of squares of (T – k) independent
is the sum of squares of (T – k) independent  random variables.
random variables.
Thus,

Also, b and  are uncorrelated, since,
are uncorrelated, since,
![\displaystyle \mathop{\mathbb E}[\hat u(b - \beta)^T] = \mathop{\mathbb E}[M_Xu u^T X (X^TX)^{-1} = 0. \ \ \ \ \ (41) \displaystyle \mathop{\mathbb E}[\hat u(b - \beta)^T] = \mathop{\mathbb E}[M_Xu u^T X (X^TX)^{-1} = 0. \ \ \ \ \ (41)](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cmathop%7B%5Cmathbb+E%7D%5B%5Chat+u%28b+-+%5Cbeta%29%5ET%5D+%3D+%5Cmathop%7B%5Cmathbb+E%7D%5BM_Xu+u%5ET+X+%28X%5ETX%29%5E%7B-1%7D+%3D+0.+%5C+%5C+%5C+%5C+%5C+%2841%29&bg=ffffff&fg=000000&s=0)
Since b and  are independent, b and
are independent, b and  are also independent.
are also independent.
2.5. t Tests about 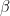 Under Above Assumptions
Under Above Assumptions
We wish to test the hypothesis that the ith element of 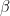 ,
,  , is some particular value
, is some particular value  .
.
The t-statistic for testing this null hypothesis is

where  denotes the ith column and ith row element of
denotes the ith column and ith row element of  and
and  is the standard error of the OLS estimate of the ith coefficient.
is the standard error of the OLS estimate of the ith coefficient.
Under the null hypothesis,

Thus,

Thus,

Thus the numerator is N(0, 1) and the denominator is the square root of a chi-square distribution with (T – k) degrees of freedom. This gives a t-distribution to the variable on the left side.
2.6. F Tests about 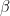 Under Above Assumptions
Under Above Assumptions
To generalize what we did for t tests, consider that we have a matrix 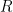 that represents the restrictions we want to impose on
that represents the restrictions we want to impose on 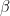 , that is
, that is  gives a vector of the hypothesis that we want to test. Thus,
gives a vector of the hypothesis that we want to test. Thus,

Since,

Thus, under  ,
,

Theorem 1 If  is a
is a  vector with
vector with  and non singular
and non singular  , then
, then  .
.
Applying the above theorem to the  vector, we have,
vector, we have,

Now consider,

where sigma has been replaced with the sample estimate s.
Thus,
![\displaystyle F = \frac{[(Rb - r)^T (\sigma^2R(X^TX)^{-1}R^T)^{-1}(Rb - r)] / m}{[RSS / (T - k)]/ \sigma^2} \ \ \ \ \ (51) \displaystyle F = \frac{[(Rb - r)^T (\sigma^2R(X^TX)^{-1}R^T)^{-1}(Rb - r)] / m}{[RSS / (T - k)]/ \sigma^2} \ \ \ \ \ (51)](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+F+%3D+%5Cfrac%7B%5B%28Rb+-+r%29%5ET+%28%5Csigma%5E2R%28X%5ETX%29%5E%7B-1%7DR%5ET%29%5E%7B-1%7D%28Rb+-+r%29%5D+%2F+m%7D%7B%5BRSS+%2F+%28T+-+k%29%5D%2F+%5Csigma%5E2%7D+%5C+%5C+%5C+%5C+%5C+%2851%29&bg=ffffff&fg=000000&s=0)
In the above, the numerator is a  distribution divided by its degree of freedom and the denominator is a
distribution divided by its degree of freedom and the denominator is a  distribution divided by its degree of freedom. Since b and
distribution divided by its degree of freedom. Since b and  are independent, the numerator and denominator are also independent of each other.
are independent, the numerator and denominator are also independent of each other.
Hence, the variable on the left hand side has an exact  distribution under
distribution under  .
.
.
be a linear function of
and
.
only depends on
and not on other previous
s.
as a deterministic number and later on we will analyse the effects of treating it as a random variable.
on
. This can be obtained by differentiating equation 10 with respect to
.
.