Type Theory – Mathematical Preliminaries

1. Sets, Relations and Functions

Definition 1 Countable Set: A set is countable if it can be placed in one-to-one correspondence with the set of natural numbers ${\mathbb{N}}$ .

Definition 2 n-place Relation: An n-place relation on a collection of sets ${\mathcal{S}_1, \mathcal{S}_2, \dotsc, \mathcal{S}_n}$ is a set ${R}$ of tuples ${R \subseteq \mathcal{S}_1 \times \mathcal{S}_2 \times \dotsc \times \mathcal{S}_n}$ . We say that elements ${s_1 \in \mathcal{S}_1}$ through ${s_n \in \mathcal{S}_n}$ are related by ${R}$ if ${(s_1, s_2, \dotsc, s_n) \in R}$ .

Definition 3 Predicates: A one place relation is also called a predicate. One-place relation on a set ${\mathcal{S}}$ is a subset ${P}$ of ${\mathcal{S}}$ . It is written as ${P(s)}$ instead of ${s \in P}$ .

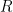
Definition 4 Binary Relation: A two place relation on sets ${\mathcal{S}}$ and ${\mathcal{T}}$ is also called a binary relation on the two sets. It is written as ${s}$ ${R}$ ${t}$ instead of ${(s, t) \in R}$ .

Three or more place relations are written using the mixfix syntax. The elements are separated by symbols. For example, ${\Gamma \dashv \mathsf{s} : \mathsf{T}}$ stands for the triple ${(\Gamma, \mathsf{s}, \mathsf{T})}$ .

Definition 5 Domain: The domain of a relation is the set of elements from the first set which are present in the tuples in the relation set.

Definition 6 Range: The domain of a relation is the set of elements from the first set which are present in the tuples in the relation set.

Definition 7 Partial Function: A binary relation ${R}$ is a partial function if, whenever ${(s, t_1) \in R}$ and ${(s, t_2) \in R}$ , then, we have ${t_1 = t_2 }$ .

Definition 8 Total Function: A partial function ${R}$ is also a total function if the domain of R is the whole set.

Definition 9 A partial function ${R}$ is said to be defined for an element ${s \in \mathcal{S}}$ if ${(s, t) \in R}$ for some ${t \in \mathcal{T}}$ . Otherwise, we write ${f(x)\uparrow}$ or ${f(x) = \uparrow}$ to mean “ ${f}$ is undefined on ${x}$ ”.

2. Ordered Sets

Definition 10 Reflexive Relation: A binary relation ${R}$ on ${\mathcal{S}}$ is said to be reflexive if ${(s, s) \in R}$ for all ${s \in \mathcal{S}}$ .

Reflexiveness only makes sense for binary relations defined on a single set.

Definition 11 Symmetric Relation: A binary relation ${R}$ on ${\mathcal{S}}$ is said to be symmetric if ${(s, t) \in R \Rightarrow (t, s) \in R}$ for all ${s, t \in \mathcal{S}}$ .

Definition 12 Transitive Relation: A binary relation ${R}$ on ${\mathcal{S}}$ is said to be transitive if ${(s, t) \text{ and } (t, u) \in R \Rightarrow (s, u) \in R}$ for all ${s, t, u \in \mathcal{S}}$ .

Definition 13 Anti-Symmetric Relation: A binary relation ${R}$ on ${\mathcal{S}}$ is said to be anti-symmetric if ${(s, t) \in R \text{ and } (t, s) \in R \Rightarrow s = t}$ for all ${s, t \in \mathcal{S}}$ .

Definition 14 Preorder: A reflexive and transitive relation on a set is called a preorder on that set. Preorders are usually written using symbols such as ${\leq}$ or ${\sqsubseteq}$ .

Definition 15 Partial Order: A preorder which is also anti-symmetric is called a partial order.

Definition 16 Total Order: A partial order with the property that for every two elements ${s, t \in \mathcal{S}}$ we have either ${s \leq t}$ or ${s \geq t}$ .

Definition 17 Join of two elements: It is the lowest upper bound for the set of elements which are greater than given two elements with respect to the partial order.

Definition 18 Meet of two elements: It is the greatest lower bound for the set of elements which are smaller than given two elements with respect to the partial order.

Definition 19 Equivalence Relation: A binary relation on a set is called an equivalence relation if it is reflexive, symmetric and transitive.

Definition 20 Reflexive Closure: A reflexive closure of a binary relation ${R}$ on a set ${\mathcal{S}}$ is the smallest reflexive relation ${R'}$ which contains ${R}$ . (Smallest in the sense that if some other reflexive relation ${R''}$ also contains ${R}$ then ${R' \subset R''}$ ).

Definition 21 Transitive Closure: A transitive closure of a binary relation ${R}$ on a set ${\mathcal{S}}$ is the smallest transitive relation ${R'}$ which contains ${R}$ . (Smallest in the sense that if some other transitive relation ${R''}$ also contains ${R}$ then ${R' \subset R''}$ ). It is written as ${R^{+}}$ .

Definition 22 Sequence: A transitive closure of a binary relation ${R}$ on a set ${\mathcal{S}}$ is the smallest transitive relation ${R'}$ which contains ${R}$ . (Smallest in the sense that if some other transitive relation ${R''}$ also contains ${R}$ then ${R' \subset R''}$ ). It is written as ${R^{+}}$ .

Definition 23 Permutation: A transitive closure of a binary relation ${R}$ on a set ${\mathcal{S}}$ is the smallest transitive relation ${R'}$ which contains ${R}$ . (Smallest in the sense that if some other transitive relation ${R''}$ also contains ${R}$ then ${R' \subset R''}$ ). It is written as ${R^{+}}$ .

Definition 24 Decreasing Chain: A transitive closure of a binary relation ${R}$ on a set ${\mathcal{S}}$ is the smallest transitive relation ${R'}$ which contains ${R}$ . (Smallest in the sense that if some other transitive relation ${R''}$ also contains ${R}$ then ${R' \subset R''}$ ). It is written as ${R^{+}}$ .

Definition 25 Well Founded Preorder: A transitive closure of a binary relation ${R}$ on a set ${\mathcal{S}}$ is the smallest transitive relation ${R'}$ which contains ${R}$ . (Smallest in the sense that if some other transitive relation ${R''}$ also contains ${R}$ then ${R' \subset R''}$ ). It is written as ${R^{+}}$ .

3. Induction

Axiom (Principle of Ordinary Induction) Suppose that ${P}$ is a predicate defined on natural numbers. Then:

If ${P(0)}$

and, for all ${i}$ , ${P(i)}$ implies ${P(i + 1)}$ ,

then, ${P(n)}$ holds for all ${n \in N}$ .