Confidence Interval Interpretation – Gaurav Sharma's Blog

In frequentist statistics (which is one the used by journals and academia), ${\theta}$ is a fixed quantity, not a random variable.

Hence, a confidence interval is not a probability statement about ${\theta}$ .

A 95 percent confidence interval does not mean that the interval would capture the true value 95 percent of the time. This statement would be absurd, because the experiment is conducted after assuming that the ${\theta}$ is a fixed quantity (which is the basic assumption we need while doing frequentist inference).

A sample taken from a population cannot make probability statements about ${\theta}$ , which is the parameter of the probability distribution from which we derived the sample.

The 95 in a 95 percent confidence interval only serves to give us the percentage of time the confidence interval would be right, across trials of all possible experiments, including the ones which are not about this ${\theta}$ parameter that is being discussed.

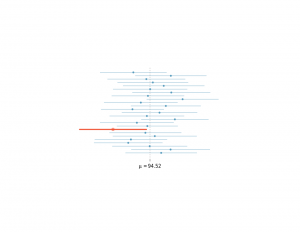
Confidence Interval Meaning

As an example, on day 1, you collect data and construct a 95 percent confidence interval for a parameter ${\theta_1}$ .

On day 2, you collect new data and construct a 95 percent confidence interval for an unrelated parameter ${\theta_2}$ . On day 3, you collect new data and construct a 95 percent confidence interval for an unrelated parameter ${\theta_3}$ .

You continue this way constructing confidence intervals for a sequence of unrelated parameters ${\theta_1, \theta_2, \dotsc, \theta_n}$ .

Then 95 percent of your intervals will trap the true parameter value.