Probability

1. Introduction

Probability is the mathematical language for quantifying uncertainty.

2. Sample Space and Events

The setup begins with an experiment being conducted. It can have a number of outcomes. The following are then defined:

Definition 1

  • Sample Space: The sample space {\Omega} is the set of all possible outcomes.

    • Definition 2

  • Realizations, Sample Outcomes or Elements: These refer to points {\omega} in {\Omega}.

    • Definition 3

  • Events: Subsets of sample space are called events.

    • Example 1 If we toss a coin twice then {\Omega = \lbrace HT, TH, HH, TT\rbrace} and the event that the first toss is heads is {A = \lbrace HH, HT\rbrace}.

    The complements, unions, intersections and differences of event sets can be defined and interpreted trivially. {\Omega} is the true event and {\emptyset} is the false event.

    Definition 4

  • Disjoint or Mutually Exclusive Events: {A_1, A_2, \dotsc,} are mutually exclusive events if {A_i \bigcap A_j = \emptyset} whenever {i \neq j}.

    • Definition 5

  • Partition of {\Omega}: A partition of {\Omega} is a sequence of disjoint sets such that their union is {\Omega}.

    • 3. Probability

    Definition 7

  • Probability Distribution or a Probability Measure: A function {\mathbb{P}} is called a probability measure or a probability distribution if it satisfies the following three axioms:
  • Axiom 1: {\mathbb{P}(\Omega) = 1}.
  • Axiom 2: {\mathbb{P}(A) \geq 0} for every {A}.
  • Axiom 3: If {A_1, A_2, \dotsc, } are disjoint, then:

    \displaystyle \mathbb{P}\left(\bigcup \limits_{i=1}^{\infty} A_i\right) = \sum_{i=1}^{\infty}\mathbb{P}(A_i) \ \ \ \ \ (2)

    • 4. Properties of Probability Distributions

    One can derive many properties from the definition of probability distribution (Definition 7).

    \displaystyle \mathbb{P}(\emptyset) = 0 \ \ \ \ \ (3)

    \displaystyle A \subset B \Longrightarrow \mathbb{P}(A) \leq \mathbb{P}(B) \ \ \ \ \ (4)

    \displaystyle 0 \leq \mathbb{P}(A) \leq 1 \ \ \ \ \ (5)

    \displaystyle \mathbb{P}(A^c) = 1 - \mathbb{P}(A) \ \ \ \ \ (6)

    \displaystyle A \bigcap B = \emptyset \Longrightarrow \mathbb{P}\left(A \bigcup B\right) = \mathbb{P}(A) + \mathbb{P}(B) \ \ \ \ \ (7)

    Lemma 8 If {A} and {B} are two events, then

    \displaystyle \mathbb{P}\left(A \bigcup B\right) = \mathbb{P}(A) + \mathbb{P}(B) - \mathbb{P}\left(A \bigcap B\right) \ \ \ \ \ (8)

    Theorem 9 Continuity of Probabilities: If {A_n \rightarrow A}, then

    \displaystyle \mathbb{P}(A_n) \rightarrow \mathbb{P}(A) \ \ \ \ \ (9)

    as {n \rightarrow \infty}.

    5. Probability on Finite Sample Spaces

    If the sample space {\Omega = \{\omega_1, \omega_2, \dotsc, \omega_n\}} is finite and each outcome is equally likely, then:

    \displaystyle \mathbb{P}(A) = \frac{|A|}{|\Omega|} \ \ \ \ \ (10)

    Given {n} objects, the number of ways of arranging or permuting them is

    \displaystyle n! = 1 \times 2 \times \dotsb \times (n - 1) \times n \ \ \ \ \ (11)

    Given {n} objects, the number of ways of selecting or choosing {k \text{ (where } 1 \leq k \leq n)} out of them is

    \displaystyle \begin{pmatrix} n \\ k \end{pmatrix} = \frac{n!}{k!(n-k)!} \ \ \ \ \ (12)

    For example, the number of ways to chose 3 students out of a class of 20 is

    \displaystyle \begin{pmatrix} 20 \\ 3 \end{pmatrix} = \frac{20!}{3!(17)!} = \frac{20 \times 19 \times 18}{1 \times 2 \times 3} = 1140 \ \ \ \ \ (13)

    6. Independent Events

    Definition 10

  • Independent Events: Two events, {A} and {B} are said to be independent if

    \displaystyle \mathbb{P}(AB) = \mathbb{P}(A)\mathbb{P}(B) \ \ \ \ \ (14)

    A set of events {\{A_i : i \in I\} } is independent if

    \displaystyle \mathbb{P}\left(\bigcap_{i \in J} A_i\right) = \prod_{i \in J} \left(\mathbb{P}(A_i)\right) \ \ \ \ \ (15)

    for every finite subset {J} of {I}.

    • Independence can be of two types – assumed or derived.

    Two disjoint events cannot be independent.

    7. Conditional Probability

    Definition 11

  • Conditional Probability: The conditional probability of {A} given {B} has occurred is

    \displaystyle \mathbb{P}(A|B) = \frac{\mathbb{P}(A \bigcap B)}{\mathbb{P}(B)}. \ \ \ \ \ (16)

    • Remark 1 {\mathbb{P}(A|B)} is the fraction of times {A} occurs in cases when {B} has occurred.

    Lemma 12 If {A} and {B} are independent events then {\mathbb{P}(A|B) = \mathbb{P}(A)}. Also, for any pair of events {A} and {B}

    \displaystyle \mathbb{P}(AB) = \mathbb{P}(A|B)\mathbb{P}(B) = \mathbb{P}(B|A)\mathbb{P}(A). \ \ \ \ \ (17)

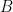
    8. Bayes’ Theorem

    Theorem 13

  • The Law of Total Probability: Let {A_1, A_2, \dotsc, A_n} be a partition of {\Omega} and let {B} be any event, then:

    \displaystyle \mathbb{P}(B) = \sum_{i=1}^n \mathbb{P}(B|A_i)\mathbb{P}(A_i). \ \ \ \ \ (18)

    • Overview of Total Probability Theorem:

    • We are given
      • a partition of the sample space and
      • any other event B.
    • We have found a relation between
      • the probability of the single event B and
      • the probabilities of the events comprising the partition and the conditional probabilities of the single event B given the events in the partition.

    Theorem 14

  • Bayes’ Theorem: Let {A_1, A_2, \dotsc, A_n} be a partition of {\Omega} such that {\mathbb{P}(A_i) > 0 } for each {i}. If {\mathbb{P}(B) > 0}, then for each {i = 1, \dotsc, n}:

    \displaystyle \mathbb{P}(A_i|B) = \frac{\mathbb{P}(B|A_i)\mathbb{P}(A_i)}{\sum_{j=1}^n \mathbb{P}(B|A_j)\mathbb{P}(A_j)}. \ \ \ \ \ (19)

    • Overview of Bayes’ Theorem:

  • Inputs: We are given
  • A partition of the sample space: A set of n events covering the sample space.
  • An other event {B}: {B} is not part of the partition.
  • Relation Found: We have found a relation between
  • Probability of {A_i|B}: The probability of the partition events given the single event {B} has occurred.
  • This has been expressed in terms of
  • Probability of {B|A_i}: The probability of the single event {B} given the partition events have occurred.

    Example 2 Suppose that {A_1, A_2 \text{ and } A_3} are the events that an email is spam, low priority or high priority, respectively. Let {\mathbb{P}(A_1) = .7, \thinspace \mathbb{P}(A_2) = .2, \text{ and } \mathbb{P}(A_3) = .1 }.

    Let {B} be the event that the email contains the word “free”.

    Let {\mathbb{P}(B|A_1) = .9, \thinspace \mathbb{P}(B|A_2) = .02, \text{ and } \mathbb{P}(B|A_3) = .01 }.

    If the email received has the word “free”, what is the probability that it is spam?

    Here,

    \displaystyle \mathbb{P}(Spam Email | Email has Word Free) = \mathbb{P}(A_1|B) \ \ \ \ \ (20)

    \displaystyle \mathbb{P}(A_1|B) = \frac{\mathbb{P}(B|A_1)\mathbb{P}(A_1)}{\sum_{j=1}^3 \mathbb{P}(B|A_j)\mathbb{P}(A_j)} = \frac{.9 \times .7}{.9 \times .7 + .01 \times .2 + .01 \times .1} = .995. \ \ \ \ \ (21)